Reliability is, perhaps, one of the biggest concerns for any data storage system. Many users understand how redundancy schemes like RAID and Windows Home Server’s Drive Extender technology protect them from data loss. These systems of data storage generally protect against hard drive failure, which is bound to occur at some point. Perhaps the best way to start off this article is to remind one that it is not if a disk will fail, but when. That “when” usually occurs at the worst possible time for a user so it is recommended that valuable data is held in redundant systems and backed-up. This article will go into the basics of redundancy. Rest assured, I have been working on something much more comprehensive, so this is just a primer. The often cited Wikipedia RAID entry is a great resource, but it is time for something a bit more detailed.
Standardizing Terminology
What does RAID Stand for?
First off, RAID stands for a Redundant Array of Independent Disks. For many users, this definition of the acronym sits juxtaposed to RAID 0’s existence as a RAID level, since RAID 0 has no redundancy. That and more will be described below.
Now that RAID is defined, here are a few more one will need while reading this article:
- MTTDL –Mean Time To Data Loss which in the below examples is simply the mean time until drive failures cause data loss in the array. Note: The below examples are perhaps the most simplistic way to view this, but the equations help.
- MTBF – Mean Time Between Failures is the mean time between hard disk failures.
- MTTR – Mean Time To Recover is the mean time to rebuild redundancy in the array.
- #Disks – Number of disks present in the array.
- k is the number of RAID 5 or RAID 6 sets that underlie a RAID 50 or RAID 60 configuration. The higher the k value, the more redundancy is built into the array.
- UBER – Unrecoverable Bit Error Rate is basically a RAID 4 or RAID 5 array’s worst enemy as an error bit could cause a failed array rebuild.
Also, I know a lot of people are going to want to take the formulae in this article and create their own Excel spreadsheet. I am on my third iteration of modeling the above and am currently adding in UBER failure to this model. Once this is added I will let everyone have a tool to do the calculations themselves. Just to give you some initial sample model output I will be including failure (disk failure related only) graphs with the following assumptions:
- Unlimited hot spares (i.e. this assumes having drives in the system to immediately start the rebuild)
- A 5 year MTBF for drives because I do not believe modern SATA drives have a 24×7 duty cycle MTBF of longer as manufacturers claim.
- A 50MB/s constant rebuild rate for all RAID types
- 15TB stored on 20 2TB drives (the 20 drives is total including the ones used for data instead of redundancy.)
There are huge faults with these assumptions, but they will at least illustrate failure rates for people. Expect more to come. You will see why big RAID 0, 4, 5, and 50 arrays scare me. Here is a quick preview using the maximum drive capacity of a Norco RPC-4020 (twenty hot swap drives with two internal drives as hotspares providing “unlimited” hotspares):

Update: The above used a 5 year MTBF. Just to give one an idea, a lot of studies find MTBF of drives in real world conditions where power supplies are not perfect, the enclosures transmit vibration, hot spares are added jostling the installed disks, and etc. Quite a few studies peg AFR at about 6%. A Seagate explanation of predicting MTBF for consumer drives shows a few characteristics of large storage systems that negatively effect drive longevity. First, to get maximum price/ capacity, people often use consumer SATA drives where the MTBF is based on a low annual power on hour rate. Increasing the power on hours to 8760 for 100% up-time over a year greatly reduces MTBF. Second, the tendency is to use large drives, making three and four platter designs more common. Oftentimes, a high density enclosure such as a Norco RPC-4220 will also have fairly warm drives due to the high density and restricted airflow. Oftentimes, drives run 15C-20C over ambient. In home and office environments with 71F and 22C temperatures that makes the drives run at 37-42C, but I have seen many installations running much warmer after disk activity and the enclosure starting to suffer from heat soak. Duty cycles depend on individual situations, but high-capacity home servers tend to have a lot of risk factors that tend to decrease MTBF significantly. Just to give one an idea of how dramatic of a change MTBF makes in Poisson models, here is a graph with a 10 year MTBF instead of a 5 year MTBF.
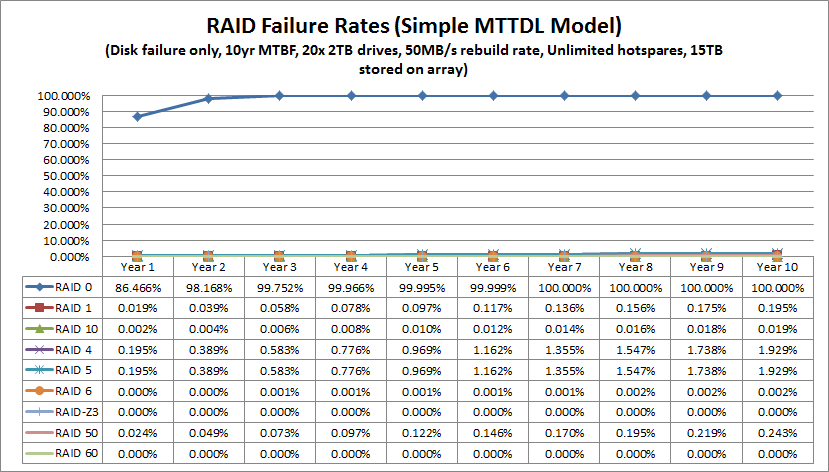
That is a really big difference. Apologies if the original numbers were confusing but I have seen this quite a bit.
RAID Levels Not Requiring Parity Calculation
Three types of RAID levels work well on almost any modern RAID controller, RAID 0, 1, and 10. The reason for this is that all of these RAID levels do their work with no need to calculate parity.
RAID 0, in a simple sense, works by taking a piece of data and parsing it out to different drives. This allows the storage controller to request data from multiple disks simultaneously, thereby circumventing the performance limitations of a single drive. In theory the sequential transfer performance is the numbers of disks multiplied by the sequential read or write speed of each disk up to the maximum speed the storage controller can handle. There is no redundancy with RAID 0 so one drive failing will render the array inaccessible and destroyed. Generally speaking, RAID 0 should only be used for data sets that one expects to fail as the chance of data loss is very high. Best practice is to have a mirror of some sort and very frequent backups of RAID 0 arrays, unless they are used solely for a cache style application where the data stored is not master data.
Minimum number of disks: 2
Capacity = Drive Capacity * #Disks
MTTDL = MTBF/ #Disks
One can see why 20 drives in RAID 0 is fairly risky, and also why nobody would do this for critical data in a live environment:

RAID 1 is perhaps the king of reliability when it comes to the simple RAID types. In RAID 1, the controller sends complete information to each disk which in turn stores a (hopefully) identical copy. Performance on most controllers is about equal to a single disk’s performance and there is little strain on modern controllers. The negative is that performance is limited to that of a single disk. When rebuilding an array however, RAID 1 arrays tend to be rebuilt relatively quickly.
Minimum number of disks: 2
Capacity = Drive Capacity / m (where m is the number of mirrored disks being used, this is usually 2)
MTTDL = (MTBF ^ #Disks) (if no time to replace is taken into account)
MTTDL = (MTBF ^ 2) / ((#Disks) * (#Disks – 1) * MTTR) (two drive mirror including time to replace)
A quick Windows Home Server note here, WHS V1 is very similar to RAID 1 in terms of redundancy. The main benefit is that files are duplicated on different drives rather than two drives being exact copies. Hence, if two drives fail in a three drive or larger system, data loss will not be 100% of the information stored on each drive. A downside to WHS technology is that the duplication of data is not always real-time. Newly written files can have duplication lag so if someone were to write a 40GB file to a WHS array, it is highly likely a single drive failure (on the disk containing the file) could cause that file to be lost if it occurs in the first few minutes or hours after that 40GB is written. Also, if one turns duplication off for a share location in WHS, that data will be susceptible to the disk containing the data’s failure. In this case the failure for non-duplicated data is simply: MTBF
Here is what RAID 1 looks like from a MTTDL perspective:

RAID 10 combines performance and redundancy by including both the striping features of RAID 0 with the redundancy of RAID 1. This is another widely used RAID level because it requires little computation on the part of the storage controller, maintains redundancy, and gives much better performance than a standard RAID 1 array.
Minimum number of disks: 4
Capacity = (Drive Capacity * #Disks) / 2
MTTDL = (MTBF ^ 2) / ((#Disks) * (#Disks – 1) * MTTR) (this is a bit too simplistic but for this article’s purpose it is close enough)
It should be noted that RAID 0 + 1 is another commonly supported RAID level. Here two RAID 0 arrays are mirrored but because the underlying arrays are RAID 0, one ends up having a fairly high chance of failure.
RAID 10’s simple model output looks like the below:

RAID Levels Requiring Parity Calculation
Other types of RAID are more strenuous on storage controllers. These arrays require the calculation of parity information for all of the data. As the number and size of disks grow, so does the potential strain on the storage controller. The trade-off is that, with a fast storage controller, these types of arrays allow for very strong performance with fewer disks overhead for redundancy. In these RAID modes, disk failure puts the array into “degraded” state meaning that upon replacement of a drive, the array will rebuild redundancy. As a result, all disks will have spare cycles dedicated to the necessary read and write operations while redundancy is restored. Further, additional disk failures, depending on RAID level, can cause all data on all disks to be lost, similar to a RAID 0 array (except initially protected from a set number of drive failures).
Single Disk Failure Redundancy
RAID 4 stores information on each disk in parallel yet calculates and stores parity information on a single disk and is considered a single parity RAID level. Single parity means that the RAID 4 array can continue to be used, data intact, after sustaining a single disk failure. This parity storage for the single disk, practically speaking, allows each member disk (aside from the one with the parity data) to be read independently of the RAID array. In catastrophic controller or other failure scenarios, partial data recovery will be facilitated by the ability to read data directly off each drive. Also, in a two drive failure scenario, RAID 4 allows the other member disks to have data recovered resulting in only, at most, two drives of data loss. Performance wise, RAID 4 generally fares poorly. Reads and writes are done to individual disks meaning the maximum throughput for copying a single file is limited by single drive speed. Furthermore the use of a single parity drive can be a bottleneck.
RAID 4 is currently used by two vendors in the home and small business space. NetApp Inc. is a major storage vendor that made RAID 4 popular alongside its proprietary Write Any Where File Layout (WAFL) system and custom made appliances to mitigate the performance issues. While NetApp still supports RAID 4 for backwards compatibility reasons, it highly encourages the use of RAID-DP, its RAID 6 implementation which will be discussed shortly. The other, significantly smaller, RAID 4 vendor is Lime Technology which uses a modified Slackware Linux core, and no custom file system, to provide a RAID 4 based NAS operating system that can be run on commodity hardware and a USB flash drive. Lime Technology is also pursuing a dual parity implementation. Performance is significantly lower than Windows Home Server, RAID 1 or other forms of RAID, but some users value the ability to recover from unaffected disks in a disaster scenario rather than use another form of RAID.
Minimum number of disks: 3
Capacity = Drive Capacity * (#Disks – 1)
MTTDL = (MTBF ^ 2) / ((#Disks) * (#Disks – 1) * MTTR) (note MTTR for RAID 4 can be fairly high because the rebuild speed is slower than fast controllers with RAID 5 or RAID 6)
Although one basically is left with a non-funtional array of disks that can be covered, and only up to two drives of data loss (assuming all other data is retrieved before the other disks fail), here is the RAID 4 simple MTTDL model graph:

There is a reason NetApp supports RAID 4 only for legacy purposes.
RAID 5, like RAID 4 is a single parity RAID level meaning that data will remain accessible through one disk failure. Unlike RAID 4, the parity information is distributed to member disks, as is the data information (in a way analogous to RAID 0 in that it distributes data). RAID 5, or a close derivative thereof, is widely adopted and implemented in hardware and software. Read performance is oftentimes very good as data is retrieved from multiple disks simultaneously. Write performance is mainly dependent on the speed at which the RAID controller (hardware and software) can calculate parity information and then the write speeds of the member disks.
One drawback of RAID 5, and RAID 4 to some extent, is the susceptibility to bit error rates (BER). With only one set of parity information, if a drive fails, and there is an error that prevents proper rebuild by using parity information, the rebuild may fail causing complete data loss even in the event of a single disk failure. With larger capacity drives, the chances of having an error rise and BER compared to drive capacity becomes a primary reason RAID 5 and RAID 4 are significantly less “safe” RAID levels than RAID 6. To put this in perspective, if a drive has an uncorrected bit error rate (UBER) of one error every 12TB that is not much for a 100GB drive. However, in a six 2TB disk RAID 5 array that has 10TB of data and 2TB of parity information, the UBER of a RAID array becomes more important.
Minimum number of disks: 3
Capacity = Drive Capacity * (#Disks – 1)
MTTDL = (MTBF ^ 2) / ((#Disks) * (#Disks – 1) * MTTR) (note this excludes the UBER portion of the calculation to keep this simple)
RAID 5’s simple MTTDL model will look just like RAID 4, except remember that a two drive RAID 5 failure means all data is lost:

77% 10 year failure chance… just say no to big arrays and RAID 4 or RAID 5. Just as a sneak preview, the above numbers get much worse when UBERs are factored in, so all of these numbers are more or less “best case.”
Double Disk Failure Redundancy
RAID 6 is probably best described as RAID 5 except with two sets of parity information being stored. This makes UBER less important because there are two sources of information if one drive fails and an error is encountered. Furthermore, RAID 6 can sustain two drive failures and still have data accessible. A downside is that twice as much parity information must be calculated by the storage controller, and an additional write must occur. RAID 5 writes data + one parity write while RAID 6 writes data plus two parity writes. Read speeds can be very high since data is striped across multiple drives as it is in RAID 5. For most storage arrays, given today’s drive capacities, I recommend RAID 6 over RAID 5 (but not necessarily over RAID 1 and RAID 10) for all modern SATA disks due to reliability concerns with RAID 5 and large drives. As mentioned earlier, NetApp’s RAID-DP is another example of RAID 6 and shows the move away from single parity configurations.
Minimum number of disks: 4
Capacity = Drive Capacity * (#Disks – 2)
MTTDL = (MTBF ^ 3) / ((#Disks) * (#Disks – 1) * (#Disks – 2) * MTTR^2) (note, again, this excludes the UBER portion of the calculation to keep this simple)

What a difference an extra drive makes! At mid-2010 prices of $100-$120/ 2TB, going RAID 6 over RAID 5 is a “no brainer” at this point. Another preview point, RAID 6 does much better dealing with the UBER part of the model.
Triple Disk Failure Redundancy (using a non-standard RAID type)
RAID-Z3 is a popular “unofficial” raid level that is worth mentioning. Basically, this is a ZFS file system (OpenSolaris and FreeBSD) exclusive RAID level that is essentially like RAID 5 or RAID 6, except with a third set of parity information. If you were wondering, RAID-Z is the RAID 5 single parity equivalent and RAID Z2 is the RAID 6 double parity equivalent. Again this is not an official RAID level, but it is popular and I wanted to show a triple redundant array type for illustrative purposes.
Minimum number of disks: 5
Capacity = Drive Capacity * (#Disks – 3)
MTTDL = (MTBF ^ 4) / ((Disks) * (Disks – 1) * (Disks – 2) * (Disks – 3) * MTTR^3) (note, again, this excludes the UBER portion of the calculation to keep this simple)
Of course, one needs to be running OpenSolaris or FreeBSD and ZFS for RAID-Z3, but triple parity is a really strong option for large consumer SATA drives.

Also, ZFS does background scrubbing so that helps a lot when it comes to weeding out errors during rebuilds. More on that later, but 0.172% 10 year failure rate versus 77.25% for RAID 4 and RAID 5. Sure it costs another $200-$240, but for a few hundred times the survival rate, it is probably worth it. The bad thing is that RAID-Z3 does use a lot more computing power, but with the focus on low power CPUs today, this will be less of an issue.
More Complex RAID Levels Requiring Parity Calculation
Two fairly common forms of RAID implementations are RAID 50 and RAID 60 whereby underlying RAID 5 or RAID 6 arrays are striped together essentially in RAID 0.
RAID 50 is simply two RAID 5 arrays striped in a RAID 0 configuration. Unlike RAID 0 where there is no redundancy, in this case each of the underlying arrays have single redundancy built-in thereby reducing the chance of failure. One major advantage of RAID 50 over RAID 5 is that one essentially doubles the number of parity disks with a minimum of two RAID 5 arrays. The negative with RAID 50 is that each RAID set is still susceptible to UBER based failure, which is not modelled in the MTTDL equations below. Some system administrators implementing RAID 50 will stripe more than two RAID 5 arrays of three drives each to provide speed and redundancy.
Minimum number of disks: 6
Capacity = Drive Capacity * (#Disks – k)
MTTDL = ((MTBF ^ 2) / ((#Disks / k) * (#Disks / k – 1) * MTTR)) * k
This is where k is equal to the number of RAID 5 arrays striped (RAID 50 requires at least two).

Much better than RAID 5 simply because there are fewer disks in the array and twice as many disks used for redundancy. Performance will be fairly good, but that is still a fairly high data loss rate.
RAID 60 is very similar to RAID 50, but with RAID 6 arrays underlying the RAID 0 stripes. As one can imagine, this setup is much more durable because it is less susceptible to the single drive failure plus unrecoverable bit error scenarios which currently endanger large SATA disks.
Minimum number of disks: 8
Capacity = Drive Capacity * (#Disks – (2 * k))
MTTDL = (MTBF ^ 3) / ((#Disks / k) * (#Disks / k – 1) * (#Disks / k – 2) * MTTR ^ 2) * k (note, again, this excludes the UBER portion of the calculation to keep this simple).
This is where k is equal to the number of RAID 6 arrays striped (RAID 60 requires at least two).
If you have read this far, you may have guessed that RAID 60 is going to look fairly great, and you would be correct:

More parity disks (four in the above model) and one gets a much better result than RAID 6 or RAID 50. An important difference between RAID 60 and RAID-Z3 is that RAID 60 is supported by lots of add-on RAID card manufacturers, making it usable in many OSes versus RAID-Z3.
Redundancy and Capacity
As a quick note, here is what the formatted capacity looks like with all of the arrays with 40TiB over 20x 2TB drives. Note, I just used a simple 92% calculation to get to the below numbers.

One can see that one loses very little capacity for RAID 6, RAID 60 and RAID-Z3 for the extra failure protection in large arrays. RAID 1 and WHS’s duplication feature, as one can see, basically end up becoming very expensive at large array sizes. Here is a view with just disks used for redundancy:

As one can see there is a big difference, in large arrays, between RAID 1 and other RAID types in terms of cost for redundancy. On the other hand, combined with the graphs above, one can see why it would be fairly crazy to use a 20 drive RAID 4 or RAID 5 array given the chance of failure versus the cost of todays consumer SATA drives.
Conclusion
This article will be updated and augmented as time progresses. I will also provide an online calculator to help determine some of the variables above. MTTDL is not a great indicator of RAID system reliability but I did want to provide some context so people can begin to understand why different RAID levels are used. Please feel free to make any comments, corrections, and/or suggestions either in comments or via the contact form. I will incorporate them as I can. Expect an improved model and tool soon!





THANKS! Now I understand why people say raid 5 is dead!
btw nice new site design
bookmarked. cannot wait to see bit error stuff. can you vary the size of the arrays too?
Awesome, thanks for that!
I was just considering raid 10
I was just reading about the “RAID 4” technology created by Lime Technology, which they call “UnRAID”. It’s a little different from RAID-4 in that the data isn’t striped across the drives. Each non-parity drive can (in theory) be removed from the array and still read. I believe they target this at media servers, with the idea that, if you lose the parity drive, you still have all your data. If any of the data drives die, you’re losses are limited to only that drive. E.g., say you have 6 data drives and 1 parity drive. You can lose the parity drive and two data drives, but still have four drives’ worth of data intact.
Matt: That is true, which is mentioned above. Between the MTBF portion here, and when the UBER results are online, you will see that single parity schemes like RAID 4 and 5 are very scary. Real-world, a RAID 4 array will have a higher MTBF failure rate versus a RAID 5 array because the rebuild speed is much slower. There is a reason RAID 4 is basically not used in enterprise storage and that the real champion is a small company selling to consmers. With ZFS in FreeNAS, there is very little reason to pay to use RAID 4 unless either you have legacy NetApp arrays.
How does UBER affect all RaidZ levels? Would zfs’ checksumming eliminate UBER?
Luke: In a word, mostly. V3 of the model is adding in error correction and scrubbing. There is still a small portion that will not get picked up though and being able to model that accurately is a bit of a challenge since it does depend on the amount of data written to the array.
Your number are wrong…. very wrong for RAID4/5
A RAID4 array with 20 2TB drives that rebuilds at 50MB/sec takes under 12 hours to rebuild from a lost drive. The likelihood of a second drive failure during that 11 hour window is much lower than what you represent.
Even using your equation:
MTTDL = (MTBF ^ 2) / ((#Disks) * (#Disks – 1) * MTTR)
where:
MTBF=5 years (43,000 hours)
MTTR=12 hours
Gives MTTDL=405,482 hours (46 years)
UBER is also not fatal to all RAID4/5 implementations in a degraded mode after a disk failure. The better implementations (such as unRAID) continue rebuilding a failed drive even if a UBER is encountered.
Running a disk reliability graph for RAID implementations to 10 years is silly. No one in their right mind would run drives that long. Just like tire and oil in your car, you replace them when their designated lifetime is up (3 to 5 years). It is called maintenance.
This article demonstrates common misunderstandings of statistic and MTBF.
A 500,000 MTBF does not mean the manufacturer is claiming the drive will last 500,000 hours. It means in a large group of drives, you will expect 1 failure per 500,000 hours of cumulative usage. It does not apply except to large populations… it does not apply to a population of 1. It doesn’t really apply well to a small population, such as 20 used in your example.
Your self-determined “5-year” MTBF confuses “service life” with MTBF. MTBF is also traditionally subject to the bathtub curve, although the degree to which it applies depends on the system. In the center “flatline” area, you have lower failure rates, and the service life for most systems is defined by that flatline area. Where the wearout rate ticks up, is where the defined service life is calculated. Don’t use tires on your car past their recommended service life just like you don’t use hard drives past their recommended service life.
How do you reconcile the claim in this article that that the 20-drive system will have a 98% chance of loss of a single drive (RAID-0 failure) in year 1 when large-scale studies have shown that the the rate of failure in year 1 is in the 6% range?
Hi Greg,
The absurd failure rates of RAID-0 in this article are due to an absurd choice of MTBF. Even taking the failure rate of consumer drives in their first year (pessimistic due to the ‘bathtub’ shape of the failure rate curve) of 3% (which has been reported in some large studies), a best guess MTBF can be calculated at about 250k hours.
Even so, the failure rate of a 20 drive RAID0 array in this situation still works out at 50% at 1 year. A 6% failure rate for a 20drive RAID 0 sounds possible for enterprise level drives in an appropriate controlled environment (it implies an MTBF of around 2.5 million hours – which is rather more than most manufacturers claim – but plausible if the drives have been ‘burned in’ for several weeks in a test system, to get past the first hump of the bathtub). It probably is appropriate for the purposes of this article to assume some reduction in MTBF due to sub-optimal conditions in a home/SOHO server.
Still, with 20 drives, it’s immediately apparent that even with super reliable drives, the risk of data loss is likely to be unacceptable. (6% in one year isn’t what I would call acceptable, unless used for temporary files).
There is another problem in this article: the failure rates for RAID arrays with parity have been miscalculated. They have been calculated with a 5 MB/s rebuild rate, leading to 4 day recovery times. This gives failure rates for RAID5/50 which have been over estimated by a factor of 10. Failure rates for RAID6/50, which have been over estimated by a factor of 100, and failure rates of RAID Z3 which have been over estimated 1000 fold.
WatchfulEye,
Yes, the absurd MTBF chosen by the author is the source of much of the problem. But also, applying a statistical function to a statistically invalid sample size of only 20 disks, is also invalid. In short, this article gets a failing grade in statistics for using MTTDL = MTBF/ #Disks where #Disks = 20.
Field testing on a population of more than 100,000 drives by Google was done using consumer-grade drives, not enterprise drives. Google uses cheap consumer-grade drives because it doesn’t care if they fail as long as they last long enough statistically. At any one time, several of Google’s drives are failed, and like the Internet, it routes around a failure. 10^-14 UREs versus 10^-16 UREs is not something Google cares to pay extra for.
Field testing on large populations is the gold standard. I agree a 6% chance of total loss of all data a year is unacceptable in an environment where loss is unacceptable, particularly where a parity drive can easily and cheaply be added to reduce that risk by orders of magnitude…. but the risk of loss based on field testing of large populations is in the 6% range, absent more specific information about the make/model/batch and field testing specific to that make/model/batch.
A 6% failure rate per year means failure probability is:
1-(1-0.06)^n
where n is the number of years you will use the drives before replacement. So RAID-0 has a 27% chance of loss for a 5 year period.
And of course, RAID is not and never was intended to be a substitute for backup. It is intended for 1) high availability (i.e. fault tolerance), 2) high speed (striping), and/or 3) logical volumes larger than individual disks (spanning).
I’m interested in seeing if the next article does similar butchering to the statistics involved in UREs as many other articles have done.
Actually, there’s nothing wrong with the statistics. The key is understanding what MTTDL actually means. We aren’t measuring the disks, so the number of disks is irrelevant as far as the the reliability of the statistics. We’ve already got the MTBF number to hand, and we’re assuming that it is correct.
MTTDL is the reciprocal of the number of ‘data loss events’ that are expected occur with a period of time. So, if you have 20 disks, it’s clearly correct to *expect* 20x as many disk failures. (In exactly the same way, as if you flip a coin 10 time, you would expect 5 heads. If you then flipped a coin 100 times, you would expect 50 heads. It should be self-evident that this is correct.) The actual risk of data loss can then be easily calculated via the Poisson distribution.
The probability of no Poisson events occurring is:
e^(-expected).
So, if your MTBF is 200k hours, and you have 10 drives operating for 10k hours – you would expect to see 10*10k/200k = 0.5 drive failures over that time period. What does 0.5 drive failures mean? It means if you repeated this experiment 100 or 1000 times (for a total of 1000 or 10000 drives) then it means that the mean number of drives that failed in each experiment would be 0.5.
Via the Poisson distribution, we can easily calculate the probability of no drive failures occuring in any one experiment. It’s simply e^-0.5 = 61%. In other words, 61% of experiments completed without losing a drive. Some lost one drive, some lost 2, and a few lost 3, 4, 5, 6, etc.
I’ve just read the google study. It came up with an annual failure rate of about 6% for individual drives (I had assumed you meant 6% AFR for a 20 drive RAID array).
This works out as an MTBF of 8760/0.06 (or approx 140k hours). If you want to be really anal about it, the correct calculation is 8760 / -ln (1-0.06) (as this is a Poisson distributed process). However, the results are so close, that its irrelevant which you use in this case.
Hmm. I just posted a long comment describing exactly why the statistics are correct – but it looks like someone has deleted the post. Here’s another go.
We aren’t trying to measure the MTBF here – we’re assuming the MTBF and asking the question: given the MTBF is x, how likely is it that y drives will last 1 year without a failure? If y is low, it doesn’t somehow make the statistics invalid.
Similarly, for RAID0, it *is* correct that MTTDL is MTBF/#disks.
MTTDL is defined as 1/(expected number of failures per hour). If you go from 2 drives to 20 drives – you’ll get 10x as many failures per hour. It’s exactly the same as how if you flip a coin 10x you’d *expect* 5 heads (even though you might get more or less). If you flip it 100x, you’d *expect* to get 10x as many heads.
From there it’s easy to calculate the likelihood of no failures in x hours. It’s simply:
(1-1/MTTDL)^x
which can be conveniently approximated as
e^-(x / MTTDL).
So, if you have 20 drives, with 150k hour MTBF (Saying 150k MTBF is the same as saying a 6% annualised failure rate)- then MTTDL is 7.5k hours. In 10000 hours, the expected number of drive failures is 1.33.
So the probability of no drive failures is simply:
e^-1.33 = 26.6%
Actually, the Poisson distribution was shown to have poor correlation with drive failure rates in the only large study I know that checked it. But at 0.06 for a single data point, it makes little difference.
The problem is applying non-discrete statical values to small populations. For example, the equation:
MTTDL = MTBF/#Drives
where #Drives = 1 is how people make nutty statements that a drive with 150K MTBF will last 17 years. Mathematically it is correct, but statistically it is as worthless as taking a poll of 1 person and using those results to predict the outcome of the Oscars.
But as originally discussed, it is all invalid because the author substituted his own self-imposed “service life” in the place of a proper MTBF.
Just got back from vacation but will change the MTBF numbers and fixed a model error. Whole point is to let people play with the model once it works well so you can plug in your own MTBF. The above assumption was just that and was just done to illustrate some of the worst case scenarios where consumer hardware is used with poor power supplies, insufficient battery backup/ surge protection and etc leading to high disk failure. That MTBF is actually from a AFR based on warranty returns for a client’s systems about four years ago. Power supplies were bad and were causing disk failures.
I see you updated the numbers thanks Patrick
WatchfulEye: You were right about 5MB/s instead of 50MB/s. I fixed that and also took into account the different amount of data per disk. I also updated the MTBF to show 10 years on all of the single RAID level graphs and a summary graph above.
Also, while I was on vacation the blog got hit buy a bunch of spam so the filters took out 1,000’s of messages. I think I found yours and restored it from the spam filter. If I did not, apologies if it got deleted. The advantage of these things is that they take out 1,000’s of those messages but occasionally take out real ones. I try to manually restore but going through that many, even after filtering can be daunting. Sorry if that happened to your post.
checked back. much better numbers. thx for taking feedback patrick
I’ve read a number of articles discussing disk volumes, including ones that advocate the use of, say, 750GB drives over 2TB drives due to a slightly lower $/GB. Such thoughts fail to consider limits on the number of available drive bays and PCI/HBA slots and the cost of arrays, both in acquisition and in the space and power they consume. Many of those contexts are on the order of an RYO home tower with, say, 6 disk bays and don’t factor in applications that require far more usable space and can easily exhaust a system with, say, 4 available x8 PCI-e slots.
The other variable you dont take into account for the MTTDL figures is the error read rate of consumer drives.
With 20 2Tb SATA desktop/consumer drive, you would almost be guaranteed of at least 1 unrecoverable read error during rebuild. So with any single parity raid setup, you are going to technically loose data, with no warnings.
Great article, I really enjoyed reading it. Is there the tool/spreadsheet available somewhere? I would enjoy playing with it a little bit :-)
Consider ZFS (using Nexenta or BSD, and soon (maybe) Linux)
MTTDL vs Space shows ZFS RAID-Z2 vs Others.
http://blogs.sun.com/relling/entry/raid_recommendations_space_vs_mttdl
A story of two MTTDL models
http://blogs.sun.com/relling/entry/a_story_of_two_mttdl
RAIDZ-3 can withstand 3 disk failures.
http://www.solarisinternals.com/wiki/index.php?title=ZFS_Best_Practices_Guide&pagewanted=all&printable=yes&printable=yes#Should_I_Configure_a_RAIDZ.2C_RAIDZ-2.2C_RAIDZ-3.2C_or_a_Mirrored_Storage_Pool.3F
Is there a view as to the maximum size / number of drives a RAID should have.
I have physical RAIDs capable of upto 24 drives support RAID6.
I’m being advised by the manufacturer that I should restrict my RAIDs to a maximum of 7 drives because of the rebuild times. Seems to me that a rebuild takes about 24 hours on a 16 bay RAID with 3Tb drives.
The RAID is set to automatically scrub so the risk is minimal.
No one should use a ZFS raid consisting of 20 disks in raidz3. That is quite bad. Here is why:
An ZFS raid consists of several groups of disks. Each group needs full redundancy, thus each group should be a raidz1 (raid5) or raidz2 (raid6) or raidz3 or mirror. Thus, collect several raidz1/raidz2/raidz3/mirror into one ZFS raid.
Also, one group of disks gives the IOPS of one single disk. If you have one raidz3 in your ZFS raid, then you have the IOPS of one disk. If have two groups in your ZFS raid, then you have the IOPS of two disks. etc. This is the reason you should never use one single raidz3 spanning 20 disks. You will get very bad IOPS performance.
It is recommended to use several groups in a ZFS raid. Each group should consist of 5-12 disks depending on the configuration of each group. A raidz3 group should use 9-12 disks. A raidz2 group should use 8 disks or so.
If you have 20 disks, then you should have 2 raidz3 groups. Each group consisting of 10 disks. Or, you can use 10 mirrors. There is more information on this on the ZFS wikipedia article.
Also, with big 5TB disks, it can take days possibly weeks before rebuilding a big raid. That stresses disks and you can see read errors, which makes you loose your entire raid.
Michael on this, I have since talked to quite a few of the reliability guys in the storage industry (who have really fancy computer models) and the general consensus on RAID-Z3 is something totally different. Triple parity using small enough sets of disks ends up more or less shifting the point of failure to other hardware including RAID controllers, motherboards, CPUs and etc. Very interesting thoughts.
Just wanted to post a quick note to say thank you for this. The comparison of MTTDL is awesome and something I haven’t seen presented in this format elsewhere. Fantastic article.